Mysteries So Bright

For God, who said, “Let light shine out of darkness,” has shone in our hearts to give the light of the knowledge of the glory of God in the face of Jesus Christ. (2 Cor. 4:6 ESV)

The nature of light is fascinating. It has a dual personality, sometimes acting as tiny particles of energy called photons, and at other times as a continuous wave like a wave in the ocean.

One way to demonstrate both natures is to shine light through two very close, tiny pinholes, or slits, in a sheet of aluminum foil.  When the light, which emerges from the two holes, falls on a screen on the other side, it forms an intricate pattern of darkness and brightness.  If one of the holes is covered over, the pattern of dark and light disappears leaving a blob of light that is brightest at the center getting dimmer as you go out from the center.

(Note: images borrowed from Google images)

These results can be explained by considering light to be like water waves with alternating peaks and valleys.  When two such waves come together, there will be regions where the peaks and valleys combine to double the heights and depths, and other regions where they cancel each other, leaving the water surface calm.  Hence the pattern of the light on the screen is explained by saying light acts like a wave.

However, if the light intensity in this demonstration is dimmed so that only sensitive light detectors in an optics laboratory can detect it, then the light photons can be counted one by one, thus showing them to be individual tiny bundles of energy, each one traveling through one hole or the other.  And yet the light lands on the screen only in the formerly bright regions, not the dark regions, thus preserving the intricate pattern.  Here is what that would look like in a time exposure of very dim light for a short time on the left, and a little longer time on the right. 

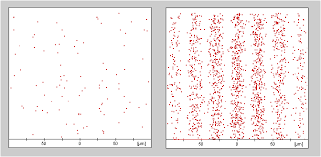
Furthermore, if one hole is covered, this pattern disappears just as before. So the mystery is: how does the particle “know” that another hole even exists when it passes through one of the holes?  The distance between the holes is very large on the scale of the size of the light particles.  And yet just the availability of a second path somehow makes the particles either reinforce each other or cancel each other out.

These results seem contradictory and have fascinated me for years.  The mathematics that physicists use can explain the effect, but it does nothing for helping our intuition about it.  There is more.  Can you believe, that a similar experiment with beams of electrons, which are tiny charged particles, show the same pattern of reinforcement and cancellation on a phosphorous screen in a darkened laboratory?  It turns out that all subatomic particles, as well as atoms and molecules, have the same dual nature, acting as waves as well as particles.  Until next time…